Table of Contents
Being one of the two pillars of modern physics, the theory of relativity is widely recognized. In addition to $E=mc^2$ (which should really be $E=\gamma (v) mc^2$) the theory of relativity covers a great range of topics, providing elegant explanations and theories that answer questions from “What is time?” to “What is inside a black hole?”. Through the journey of modern physics, the use of our imagination is crucial. We are no longer constrained to the world before our eyes.
We are no longer observing the motions of a falling metal ball or a rolling cylinder. Using our imagination, we explore the bizarre behavior of the microscopic fundamental particles, predict the faith of our universe, and travel with the speed of light. At those extremes, what will the world look like? Will the world still behave like how we think it will? In the following series of articles, I will convince you through experiments and mathematics, that the world doesn’t obey our intuition all the time. We won’t be able to answer all of the questions, but learning special relativity would be a start to answering a few of them. This study guide offers a comprehensive introduction to the world of Special Relativity. We will first introduce the idea of Galilean Relativity, reference frames. We would then examine the postulates of special relativity, and work through some problems. For those of you that are more mathematically inclined, you may proceed to relativistic electrodynamics, where we shall attempt to establish Maxwell’s equations in relativistic terms. We will also introduce the mathematical tool of four-vectors and some notation that would allow you to do much more at your own leisure.
Inertial Reference Frames
The concept of reference frames, or RF for short, is crucial in the understanding of relativity. But luckily, it is by no means a difficult concept. Suppose you and your friend each perform an identical physics experiment, tossing a ball. You stand still on the ground while your friend is in a train moving with constant velocity. You throw the ball vertically upwards and, without moving your hand, the ball lands in your hand. You friend does the exact same thing, and she achieves the same result. In this scenario, you and your friend constitutes as two different observers in two different reference frames. And the art of relativity is relating the physics in different reference frames. You and your friend in this case, are both in an special subgroup called the inertial reference frame.
An inertial reference frame is one in which an isolated particle moves at constant velocity. (There is no net force acting on said frame.)
We have mostly taken this for granted in the past. Surely, laws of physics must be the same for all! In some ways, that is true, but let us suppose the train that your friend is on, begins to accelerate. Would the ball still lands in her hand? The answer is no. From her perspective, she is stationary with respect to the train. Why doesn’t your experimental findings hold true in her frame of reference? Let’s keep this question in our minds and we shall return to it in due course. The way we switch frames of references, prior to Einstein, is via a method called Galilean transformation, part of Galileo’s formalisation of physical laws of different frames of reference, the Galilean relativity. And that is what all of this is about, special relativity included, is the relationship of physical observations done by different observers.
Back to Newton's Laws
The essence of Galilean relativity is: if Newton’s Laws of motion are true in one frame of reference, then they must be true in any other reference frame moving with constant velocity relative to the first reference frame. Hopefully now, you realised that your friend, in the second scenario, was no longer moving with constant velocity with respect to you, the first frame of reference, and thus, her frame is no longer inertial. For now, let us think of reference frames as a set of cartesian axes defined by an observer
Newton’s laws of motion can be more rigorously defined once we include the concept of an inertial frame of reference:
I. In an inertial frame, an object maintains its velocity of motion unless acted upon by an unbalanced force i.e. it moves in a straight line with constant speed.
II. In an inertial frame, an object that is acted upon by a force $\vec{F}$, changes its state of motion according to $\vec{F} = \partial_t \vec{p} = m\dv{\vec{v}}{t}$.
III. In an inertial frame, when one body exerts a force on a second body, the second body simulataneously exerts a force equal in magnitude and opposite in direction on the first body.
The third law is the equivalent in saying that the total momentum (including all objects that are creating forces, and all that are the receipients of said forces) is a constant of motion:
$$\dv{}{t}\sum_i \vec{p}_i =0$$
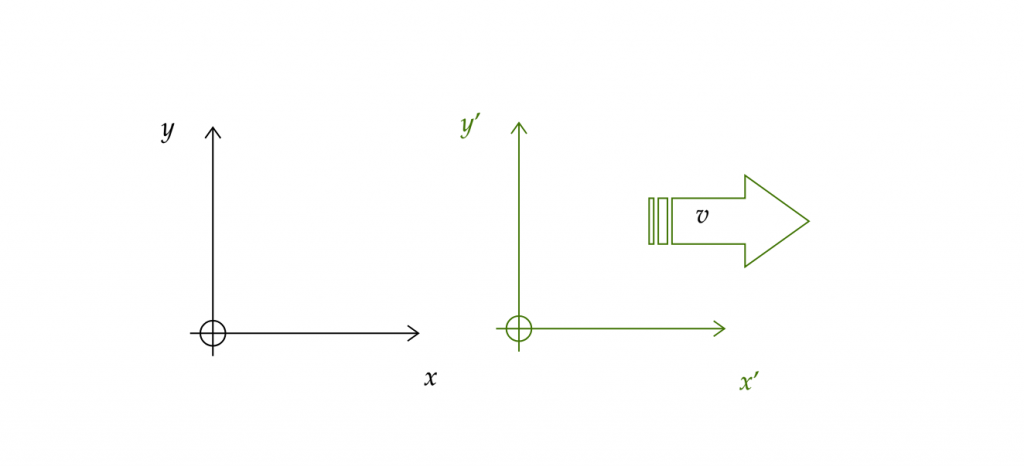
To switch between inertial reference frames, we use what is called Galilean transformation. They are defined by the followaing sets of equations:
\begin{align}t’ &= t \\ x’ &= x – vt\end{align}
The first of the two equations, $t’ = t$ represents that the concept of simple, classical time holds for both observers, that time is absolute for both observers. (As we shall see, it really isn’t.) The second of the two represents that the reference frame $x’$ is moving away in the $x$ direction with velocity $v$. It is convention to distinguish between the reference frames by adding a ‘ (prime) symbol to each of the axes in your coordinate system. Since we are only dealing with one dimensional motion for now, we can also infer that
\begin{align}y’ &= y \\ z’ &= z\end{align}
is also true.
Let us look at an example.
