Table of Contents
We are primarily concerned about smooth, continuous changes in physics. The study of dynamics is the study of things change as time passes. To do this, we will employ the math of calculus. In this short introduction, we will primarily deal with functions of time ($t$). By the end, you will be able to differentiate, and integrate relatively simple functions, more than enough for the study of rudimentary kinematics.
Limits
As we previously said, in the study of classical physics, we deal with things that change smoothly over time. A car’s velocity would be an example of smooth change. The opposite would be what we call stroboscopic change. Here is an example for each:
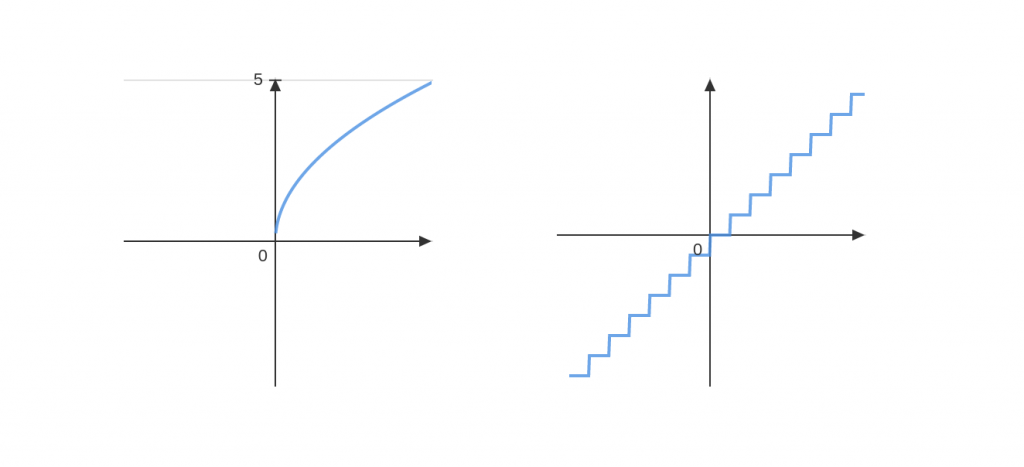
On the left, we have a smooth function, this is what we would expect how a car’s velocity would vary with time, smoothly. As compared to the graph on the right, which is not smooth and stroboscopic. For reason we shall see shortly, only functions that are smooth can be differentiated.
The concept of limits is especially important in the study of physics. To understand why, let’s first take a philosophical detour.
Zeno’s Paradox- Achilles and the Tortoise
Suppose Achilles is in a race with a tortoise. The tortoise is given a head start. Achilles, after some time, then chases after the tortoise trying to overtake it. No matter how fast Achilles can run, the tortoise never stops moving. Say Achilles catches up to the turtle in 10 seconds, but the tortoise would have travelled in those 10 seconds, no matter how little, Achilles still haven’t overtaken the tortoise. Say Achilles catches up again, in half a second, but the tortoise has travelled some more. Seemingly Achilles is stuck in this vicious cycle of catching up to the turtle but then only to find out that the turtle moved forward again. This is Zeno’s Paradox. Common sense would dictate that Achilles would overtake the tortoise easily. But physicists needed a much more concrete and rigid mathematical proof that we can indeed overtake the tortoise. Thus, the concept of limits was born. (This is an anecdote, the actual origin of limits may be something else.)
The concept of limits is simply what something is approaching. This something can be a set of numbers, a function and so on.
Let us consider the sequence of numbers, 0.9,0.99,0.999,0.999,…. Let us call this sequence $S$.
$$S_i={0.9,0.99,0.999,0.9999…}$$
$i$ is used as a counter here, so the first number in the sequence would be $S_1=0.9$, followed by $S_2=0.99$, $S_3=0.999$, and so forth…
We can find the limit of this sequence $S$, to be
\begin{equation}\lim_{i\rightarrow\infty}S_i=1\end{equation}
Equation 1 is read as ‘the limit of $S_i$ as $i$ approaches infinity equals to 1. As we are going further and further into the sequence, we can see that the numbers get infinitely close to 1, but with one caveat, none of the numbers in the sequence ever equals to one. Let’s examine another example with a function.
We know the rational function to take the form of:
$$f(x)=\frac{1}{x}$$
which has a graph that looks like this
This graph exhibits some strange behaviours near the axes, mainly because we know the fact that you can not divide a number by 0. This function has horizontal asymptote at $y=0$. So what does the function equal to then at 0? If you so dare put this in your calculator, you’d find that it would refuse to give you an answer. But let’s use limits.
$$\lim_{x\rightarrow 0}f(x)=\infty$$
Here we evaluated the limit of the function graphically, we can see that as $x$ tend to 0, the graph increases so rapidly that saying it increased exponentially would be a wild understatement.
For functions that behave themselves, like the $g(x)=x^2$, evaluating the limits is simple. We know that the graph is smooth and doesn’t have jumps. So you may evaluate the limit just by calculating it.
$$\lim_{x\rightarrow 5}x^2 = 25 = g(5)$$
The above relation only works for function that are continuous and make numerical sense. Using the previous function $f(x)=\frac{1}{x}$, here is something that is incorrect:
$$\lim_{x\rightarrow 0}=\infty=f(0)$$
Note that $f(0)\neq \infty$!
